Семь мостов Кенигсберга

Кенигсберг- Город СЕМИ МОСТОВ (раньше так называли)

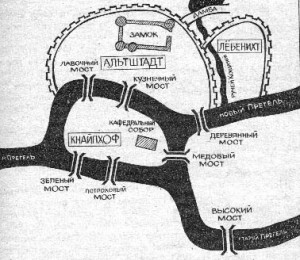
Старинная карта Кёнигсберга. Буквами обозначены части города: А — Альтштадт, Б — Кнайпхоф, В — Ломзе, Г — Форштадт. Цифрами обозначены мосты (в порядке строительства): 1 — Лавочный, 2 — Зелёный, 3 — Рабочий, 4 — Кузнечный, 5 — Деревянный, 6 — Высокий, 7 — Медовый

Лавочный мост

Самым старым из семи мостов был Лавочный мост (Krämerbrücke/Крэмер-брюке), соединявший самый главный из кёнигсбергских городов — Альтштадт с расположенным рядом кёнигсбергским замком и лежащий на острове город Кнайпхоф.

Зеленый мост

Вторым по возрасту был Зелёный мост (Grüne Brücke/Грюне-брюке).

Рабочий мост

После Лавочного и Зелёного был построен Рабочий мост (Кёттель или Киттель-брюке), также соединявший Кнайпхоф и Форштадт.

Кузнечный мост

В 1397 году был построен Кузнечный мост (Schmiedebrücke/Шмиде-брюке).

Деревянный мост

Старинный столбик из ограждения Деревянного моста. На столбике виден герб Кнайпхофа — поднятая из воды рука, держащая корону. На заднем плане — Кафедральный собор. Деревянный мост (Holzbrücke/Хольц-брюке) между Альтштадтом и Ломзе.

Высокий мост

Ещё одним сохранившимся до сих пор мостом Кёнигсберга является Высокий мост (Hohe Brücke/Хоэ-брюке).

Медовый мост

Самый молодой из семи мостов — Медовый мост (Honigbrücke/Хониг-брюке), соединяющий острова Ломзе и Кнайпхоф.

А знаете ли вы … , что Эйлер свою теорию Графов вывел думая о семи мостах Кенигсберга.

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды?

Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).

Автор Вжик